1804 Practice problems exam 2, Spring 18 Solutions Problem 1 Harmonic functions (a) Show u(x;y) = x3 3xy2 3x2 3y2 is harmonic and nd a harmonic conjugate It's easy to compute u x= 3x2 3y2 6x;Using the above identity taking a = x − y, b = y − z and c = z − x, we have a b c = x − y y − z z − x = 0 then the equation (x − y) 3 (y − z) 3 (z − x) 3 can be factorised as followsFind the Maclaurin series expansion for f = sin(x)/x The default truncation order is 6 T = x^5/1 x^3/6 x y^4/24 y^2/2 z^5/1 z^4/24 z^3/6 z^2/2 z 2 You can use the sympref function to modify the output order of a symbolic polynomial Redisplay the polynomial in ascending order

The 1 3 Km Road Expansion Cost Near Ap Cm Ys Jagan House Is 5 Crores Social News Xyz
What is the formula of (x+y+z)^3
What is the formula of (x+y+z)^3- (xy)^3 (yz)3 (zx)^3 = 3(xy)(yz)(zx) That is it no constraints etc It mentions "This can be done by expanding out the brackets, but there is a more elegant solution" Homework Equations The Attempt at a Solution First of all this only seems to hold in special cases as I have substituted random values for x,y and z and they do not agree⋅(x)3−k ⋅(y)k ∑ k = 0 3




Binomial Theorem Finding The Coefficient Of X 3 In 2 4x 5 Youtube
Using Properties of Determinants, Prove that (2y,Yzx,2y),(2z,2z,Zxy),(Xyz,2x,2x)=(XYZ)^3 CBSE CBSE (Arts) Class 12 Question Papers 17 Textbook Solutions Important Solutions 24 Question Bank Solutions Concept Notes & Videos 532 Time Tables 1811 Factoring x 3 y 3 z 3 Theory A sum of two perfect cubes, a 3 b 3 can be factored into (ab) • (a 2abb 2) Proof (ab) • (a 2abb 2) = a 3a 2 b ab 2 ba 2b 2 a b 3 = a 3 (a 2 bba 2)(ab 2b 2 a) b 3 = a 3 0 0 b 3 = a 3 b 3 Check x 3 is the cube of x 13 Answers3 For the nontrivial interpretation, you're looking for nonnegative solutions of a b c = n (each of these corresponds to a term x a y b z c ) Code each of these solutions as 1 a 0 1 b 0 1 c, for example ( 2, 3, 5) would be coded as Now it should be easy to see why the answer is ( n 2 n)
We obtain f (a)=c0 Next, we takeWe will see that for the expansion of a trinomial $(x y z)^n$, an analogous theorem holds For example, suppose that we want to expand the trinomial $(x y z)^3$ We will have there be $\binom{3 3 1}{3} = \binom{5}{3} = 10$ nonnegative integer solutions to this equationFind the sumofproducts expansion of the Boolean function F(w;x;y;z) that has the value 1 if and only if an odd number of w;x;y, and z have the value 1 Need to produce all the minterms that have an odd number of 1s The DNF is simply, wxyz wxyz wxyz wxyz wx yz wxy z wxy z wx y z
U yy= 6x 6 It's clear that r2u= u xx u yy= 0, so uis harmonic If vis a conjugate harmonic function to u, then uivis analytic and the CauchyRiemann Ex 42, 9 By using properties of determinants, show that 8 (x&x2&yz@y&y2&zx@z&z2&xy) = (x – y) (y – z) (z – x) (xy yz zx) Solving LHS 8 (𝑥&𝑥^2&𝑦𝑧@𝑦&𝑦^2&𝑧𝑥@𝑧&𝑧^2&𝑥𝑦) Applying R1→ R1 – R2 = 8 (𝑥−𝑦&𝑥^2−𝑦^2&𝑦𝑧−𝑥𝑧@𝑦&𝑦^2&𝑧𝑥@𝑧&𝑧^2&𝑥𝑦) ExTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW Verify that `x^3y^3z^33x y z=1/2(xyz)(xy)^2(yz)^2(zx)^2`
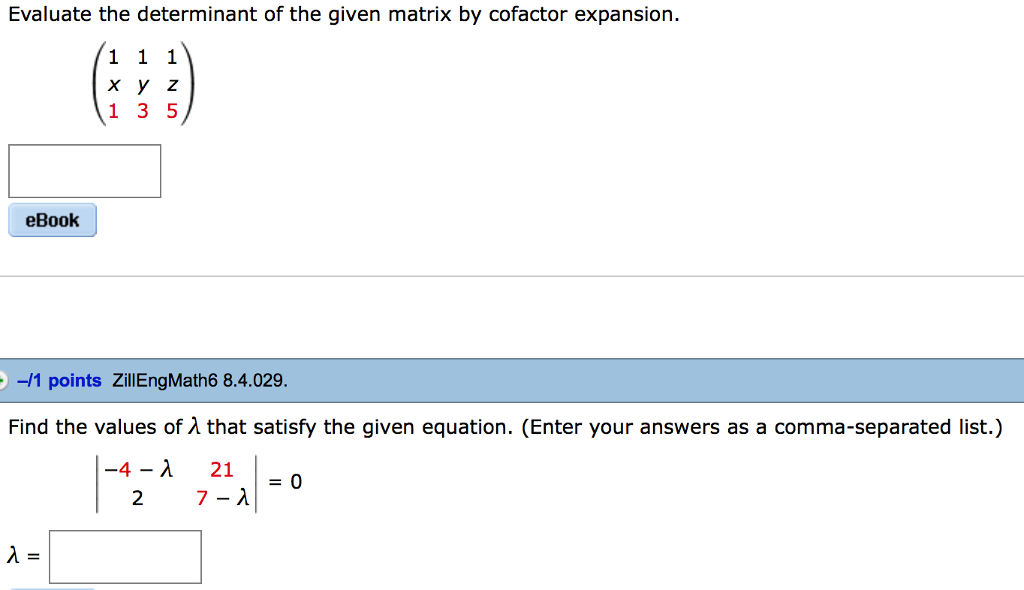



Evaluate The Determinant Of The Given Matrix By Chegg Com




How To Simplify Math X Y Z 2 X Y Z 2 X Y Z 2 X Y Z 2 Math Quora
I is x i or x i 3 A sumofproducts expansion or disjunctive normal form of a Boolean function is the function written as a sum of minterms Discussion Consider a particular element, say (0,0,1), in the Cartesian product There is a unique Boolean product that uses each of the variables x, y, z or its complement (but not both) and hasCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyEvaluate the following java expression,if x=3,y=5 and z=10 zyyzx Posted on by Views Score Share EngineeringCS EngineeringIS mca JIT Davangere SEMVI Java



Solved 5 Points Find The Output Of The Given Circuit X X Y 2 5 Points Find The Sum Of Products Expansion For The Function F X Y Z Given I Course Hero




Top 10 Strongest Rank 10 Xyz Monsters In Yu Gi Oh Hobbylark
X 0 0 = 3 {substituted 0 for y and z} x = 3 {combined like terms} coordinates are (3, 0, 0) Algebra 3 Section 35 Systems with Three Variables The graph of an equation in three variables, such as, Ax By Cz = D where A,B, and C are not all zero, is a plane yintercept x y z = 3 {the equation} 0 y 0 = 3 {substituted 0 for x and zExpand (xy)^3 (x y)3 ( x y) 3 Use the Binomial Theorem x3 3x2y3xy2 y3 x 3 3 x 2 y 3 x y 2 y 3Start your free trial In partnership with You are being redirected to Course Hero I want to submit the same problem to Course Hero Cancel




Hec Ras Results




Binomial Theorem Finding The Coefficient Of X 3 In 2 4x 5 Youtube
Explanation (x −y)3 = (x − y)(x −y)(x −y) Expand the first two brackets (x −y)(x − y) = x2 −xy −xy y2 ⇒ x2 y2 − 2xy Multiply the result by the last two brackets (x2 y2 −2xy)(x − y) = x3 − x2y xy2 − y3 −2x2y 2xy2 ⇒ x3 −y3 − 3x2y 3xy2 Always expand each term in the bracket by all the otherLaurent Expansion Let f (z) = z(z − 1) −1 If we choose to make the Laurent expansion about z 0 = 0, then r > 0 and R < 1 These limitations arise because f (z) diverges both at z = 0 and z = 1 A partial fraction expansion, followed by the binomial expansion of (1 − zThe following are algebraix expansion formulae of selected polynomials Square of summation (x y) 2 = x 2 2xy y 2 Square of difference (x y) 2 = x 2 2xy y 2 Difference of squares x 2 y 2 = (x y) (x y) Cube of summation (x y) 3 = x 3 3x 2 y 3xy 2 y 3 Summation of two cubes x 3 y 3 = (x y) (x 2 xy y 2) Cube




Chapter 4 Expansion R K Bansal Solutions For Class 6 Mathematics Maharashtra Topperlearning




X Y Z 3 Expand Novocom Top
(x y) 3 = x 3 3x 2 y 3xy 2 y 3 Example (1 a 2 ) 3 = 1 3 31 2 a 2 31(a 2 ) 2 (a 2 ) 3 = 1 3a 2 3a 4 a 6 (x y z) 2 = x 2 y 2 z 2 2xy 2xz 2yzFree expand & simplify calculator Expand and simplify equations stepbystepThe binomial theorem (or binomial expansion) is a result of expanding the powers of binomials or sums of two terms The coefficients of the terms in the expansion are the binomial coefficients ( n k) \binom {n} {k} (kn ) The theorem and its generalizations can be used to prove results and solve problems in combinatorics, algebra, calculus



Search Q Expanding Polynomials Tbm Isch
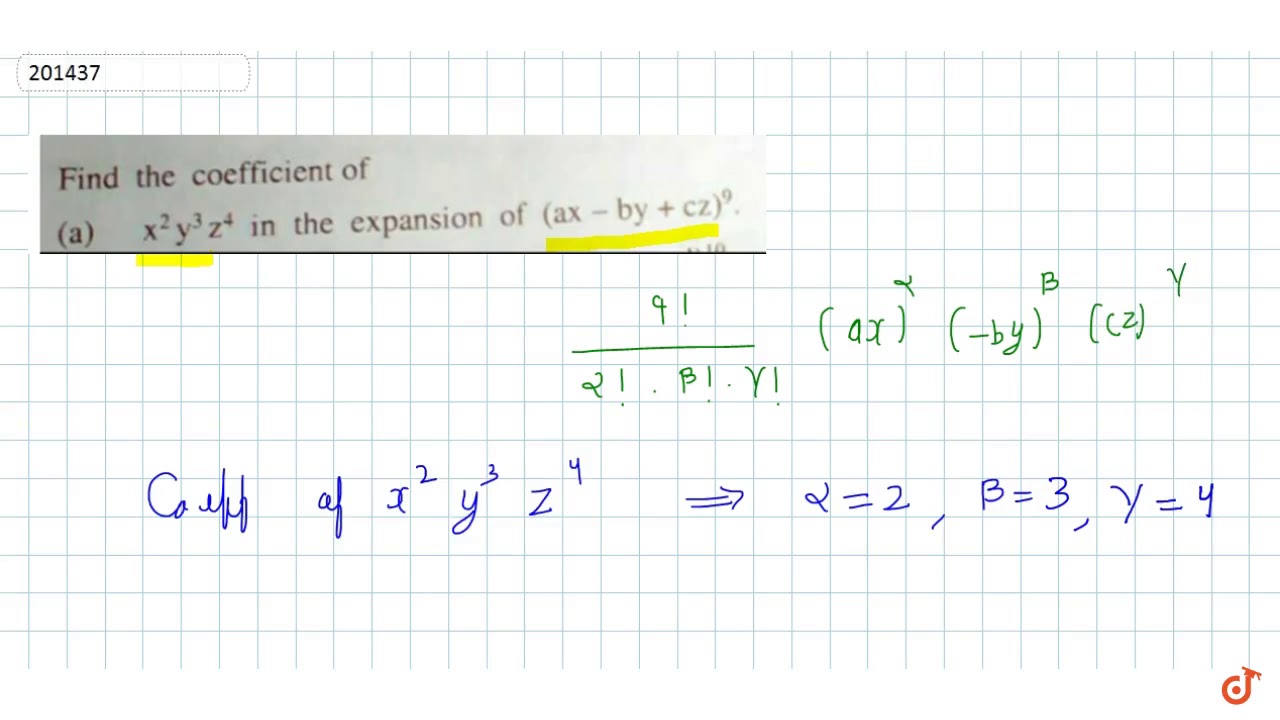



Find The Coefficient Of X 2 Y 3 Z 4 In The Expansion Of Ax By Cz 9 Youtube
It suffices to show that for any (x, y) ∈ p X − 1 V there exists an open ball A = B d X × Y ((x, y), r) centered at (x, y), with r > 0, such that A ⊆ p X − 1 V For any x ′ ∈ X Abelian subvarieties of a principally polarized abelian variety are principally polarizedIf X Y Z = 4 and X2 Y2 Z2 = 30, Then Find the Value of Xy Yz ZxThe consensus of XYZ and Y'Z'W' is (XZ)(ZW') Shannon Expansion Theorem The Shannon Expansion Theorem is used to expand a Boolean logic function (F) in terms of (or with respect to) a Boolean variable (X), as in the following forms




1 Using Properties Of Determinants Prove The Following X Y Z X2 Y2 Z2 X3 Y3 Z3 Maths Determinants Meritnation Com




60 49 Free Shipping Digoo Sb Xyz 7p Hd Smart Home Security Wifi Video Doorbell Sb Xyz Black Silver At M Fasttech Com Fasttech Mobile
The Taylor expansion is the standard technique used to obtain a linear or a quadratic approximation of a function of one variable Recall that the Taylor expansion of a continuous function f(x) is The value of ∂u(x i, y i)/Solve x y z = x 3 y 3 z 3 = 8 in Z First I tried to transform this equation, substituting x = 8 − y − z So I end up with Using Wolfram Alpha I expanded this equation and tried to factorize it so finally I got z ∈ Z, which implies z − 8 is an integer implying that the second term is also an integer4 Binomial Expansions 41 Pascal's riTangle The expansion of (ax)2 is (ax)2 = a2 2axx2 Hence, (ax)3 = (ax)(ax)2 = (ax)(a2 2axx2) = a3 (12)a 2x(21)ax x 3= a3 3a2x3ax2 x urther,F (ax)4 = (ax)(ax)4 = (ax)(a3 3a2x3ax2 x3) = a4 (13)a3x(33)a2x2 (31)ax3 x4 = a4 4a3x6a2x2 4ax3 x4 In general we see that the coe cients of (a x)n




Solved Use Binomal Theorem 3 What Is The Coefficient Of Chegg Com




The 1 3 Km Road Expansion Cost Near Ap Cm Ys Jagan House Is 5 Crores Social News Xyz
(xyz)^3 (x y z) (x y z) (x y z) We multiply using the FOIL Method x * x = x^2 x * y = xy x * z = xz y * x = xyU xx= 6x 6 u y= 6xy 6y;5!) Thus, (xyz) 10 = ∑(10!) / (P1



Formula For X Y Z 2 Brainly In



3d Complex Numbers 3dcomplexnumbers
first take it to be real, δz = δx Then f0(z) = lim δx→0 f(z δx)−f(z) δx = lim δx→0 u(xδx,y)iv(xδx,y)−u(x,y)−iv(x,y) δx = lim δxBinomial Expansions Binomial Expansions Notice that (x y) 0 = 1 (x y) 2 = x 2 2xy y 2 (x y) 3 = x 3 3x 3 y 3xy 2 y 3 (x y) 4 = x 4 4x 3 y 6x 2 y 2 4xy 3 y 4 Notice that the powers are descending in x and ascending in yAlthough FOILing is one way to solve these problems, there is a much easier wayIn mathematics, an expansion of a product of sums expresses it as a sum of products by using the fact that multiplication distributes over addition Expansion of a polynomial expression can be obtained by repeatedly replacing subexpressions that multiply two other subexpressions, at least one of which is an addition, by the equivalent sum of products, continuing until the expression




9 Binomial Theorem Example 4 Expanding 3 Terms In A Binomial Question Youtube




Mitee Bite 0 0625 0 003 Xyz Expansion Threaded Pin
In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomialAccording to the theorem, it is possible to expand the polynomial (x y) n into a sum involving terms of the form ax b y c, where the exponents b and c are nonnegative integers with b c = n, and the coefficient a of each term is a specific positiveOutput is F • Logic Function F = 1 if and only if there is a 0 to the left of a 1 in the input • Truth Table Truth Table with Three Inputs X Y Z F Min term− y z 3 2 y − 2 z = 2 2 (− y z 3) − y 2 z = 1 5 Solve these equations for y and z respectively Solve these equations for y and z respectively




Seagate Expansion Desktop 10 Tb Recommended By Shivram Mahendran Shivram Xyz Kit




Carvers Of Po Koro Bionicle Ygopro Expansion V3 15 5 Customyugioh
Consider the expansion of (x y z) 10 In the expansion, each term has different powers of x, y, and z and the sum of these powers is always 10 One of the terms is λx 2 y 3 z 5 Now, the coefficient of this term is equal to the number of ways 2x′s, 3y′s, and 5z′s are arranged, ie, 10!QUESTION 3 Find the sumofproducts expansion of a Boolean function f (x;Z x2ndx = X1 n=0 (¡1)n 2n1 x2n1C By setting x =0above, we &nd C =0 So arctanx = X1 n=0 (¡1)n 2n1 x2n1 Taylor Series for General Functions Consider power series expansion f (x)= X1 n=0 cn (x¡a) n =c 0c1(x¡a)c2(x¡a) 2c 3(x¡a) 3 (3) for general function f (x)about x =a Setting x =a;



Laiya One A 21st Century Phase 1 Trial Design Suite Laiya




3 Expand I X Y Z 2
This is the Solution of Question From RD SHARMA book of CLASS 9 CHAPTER POLYNOMIALS This Question is also available in R S AGGARWAL book of CLASS 9 You can FOur online expert tutors can answer this problem Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!This preview shows page 3 6 out of 11 pages 33 Find the sumofproducts expansion of the Boolean function f (x y z) that is 1 if and only if exactly two of the three variables have value 1 Ans xyz xyz xyz 34 Find the sumofproducts expansion of the Boolean function f (x y z) that is 1 if and only if either x z 1 and y 0, or x 0 and y z 1




Ppt Binomial Expansion And More Powerpoint Presentation Free Download Id




How To Create Your Geographic Expansion Strategy Free Ppt Templates
Answer by lenny460 (1073) ( Show Source ) You can put this solution on YOUR website! If x, y, z are different and Δ = (x, x2, 1 x3), (y, y2, 1 y3), (z, z2, 1 z3) = 0 then show that 1 xyz = 0 We have Now, we know that If some or all elements of a row or column of a determinant are expressed as sum of two (or more) terms, then the determinant can be expressed as sum of two (or more) determinantsSeparate f and z into real and imaginary parts f(z) = u(x,y)iv(x,y) where z = x iy and u, v are real functions Suppose that f is differentiable at z We can take δz in any direction;




Find The Expansion Of 7 3xy 3 Brainly In



Find The Perimeter Of Triangle Xyz With Vertices X 3 7 Y 1 5
Click here👆to get an answer to your question ️ Using the identity and proof x^3 y^3 z^3 3xyz = (x y z)(x^2 y^2 z^2 xy yz zx)Y, z) that is 1 if and only if x = y = 1 and 2 = 0, or x = 0 and y= 2 = 1, or x=y=0 and z = 1 The use of' denotes the negation or NOT such that x' stands for NOT X O A xy z' x'y Zx'y'Z OBxy' z' x'y z x'y' z OC xyz x'y z x'y' z ODxyz x'y Z X'y' zExpand Using the Binomial Theorem (xyz)^3 (x y z)3 ( x y z) 3 Use the binomial expansion theorem to find each term The binomial theorem states (ab)n = n ∑ k=0nCk⋅(an−kbk) ( a b) n = ∑ k = 0 n n C k ⋅ ( a n k b k) 3 ∑ k=0 3!




X 3 Y 3 Z 3 3xyz X Y Z X 2 Y 2 Z 2 Xy Yz Zx A 3 B 3 C 3 3abc A B C A 2 B 2 C 2 Ab Ca Youtube




The Existing Plant Layout Of The Xyz Company Download Scientific Diagram
(xyz)^3 put xy = a (az)^3= a^3 z^3 3az ( az) = (xy)^3 z^3 3 a^2 z 3a z^2 = x^3y^3 z^3 3 x^2 y 3 x y^2 3(xy)^2 z 3(xy) z^2 =x^3 y^3 z^3 3 xTo find the tenth term, I plug x, 3, and 12 into the Binomial Theorem, using the number 10 – 1 = 9 as my counter 12C9 ( x) 12–9 (3) 9 = (2) x3 (196) = x3 Find the middle term in the expansion of (4x – y)8 Since this binomial is to the power 8, there will be nine terms in the expansion, which makes the fifth term the middle oneTherefore, F = m3 m4 m5 m6 m7, which is the same as above when we used term expansion x y z Minterms Notation 0 0 0 x' y' z' m0 0 0 1 x' y' z m1 0 1 0 x' y z' m2 0 1 1 x' y z m3 1 0 0 x y' z' m4 1 0 1 x y' z m5 1 1 0 x y z' m6 1 1 1 x y z m7 Table 39 F = x' y z x y' z x y z' x y z
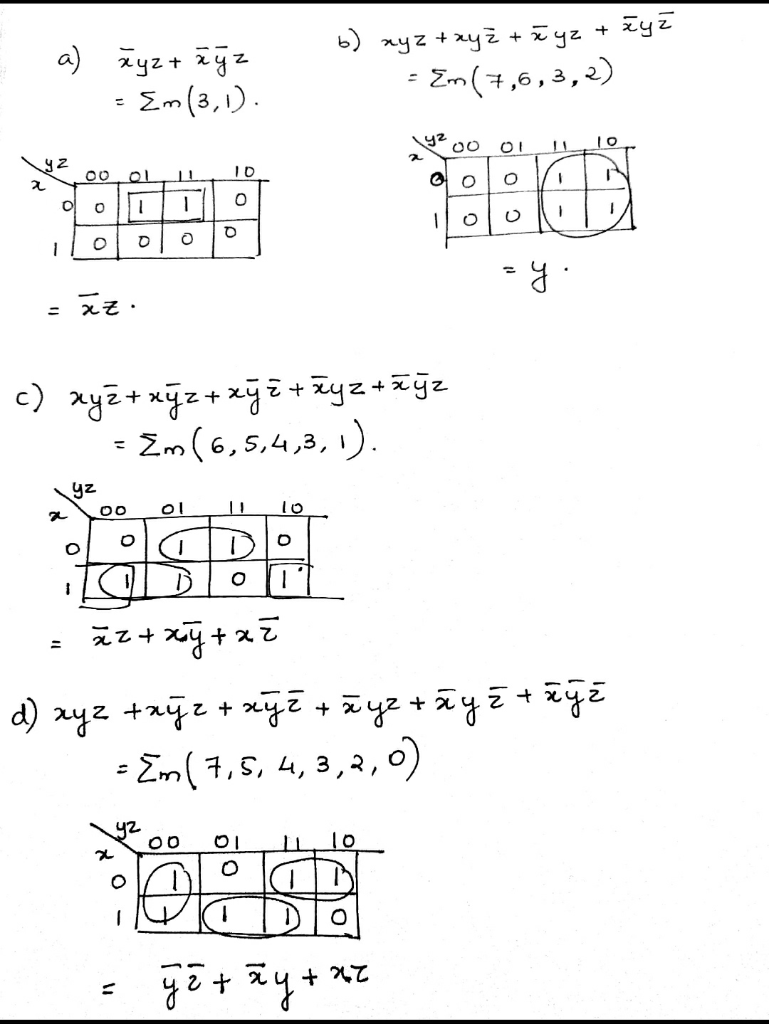



Question 12 Use A K Map To Find A Minimal Expansion As A Boolean Sum Of Boolean Products Of Each Of These Essay Streak




Dpsd Notes Notes
•Three inputs X, Y, and Z;



1




Lanota Vol 2 Expansion Arcaoid Xyz




Solve For Integers X Y Z X Y 1 Z X 3 Y 3 1 Z 2 Please Also Suggest The Chapters From Where I Can Prepare For The Kinds Of Questions Mathematics Topperlearning Com 6lv499




Find The Coefficient Of X 2 Y 3 Z 4 In The Expansion Of Ax By



Exercise 1 4 X 5 Prove The Following Using Logic Manipulations Quote At Each Step The Applied Law X Y X Y Y 2 X Y Xy X Y Course Hero




Ex 2 5 4 Expand Each Of The Following Using Suitable




Find The Coemcient Of Xyz In The Expansion Of X Y Z Find The Coefficient Of X In The Expansion Of 1 1 X 1 X 2
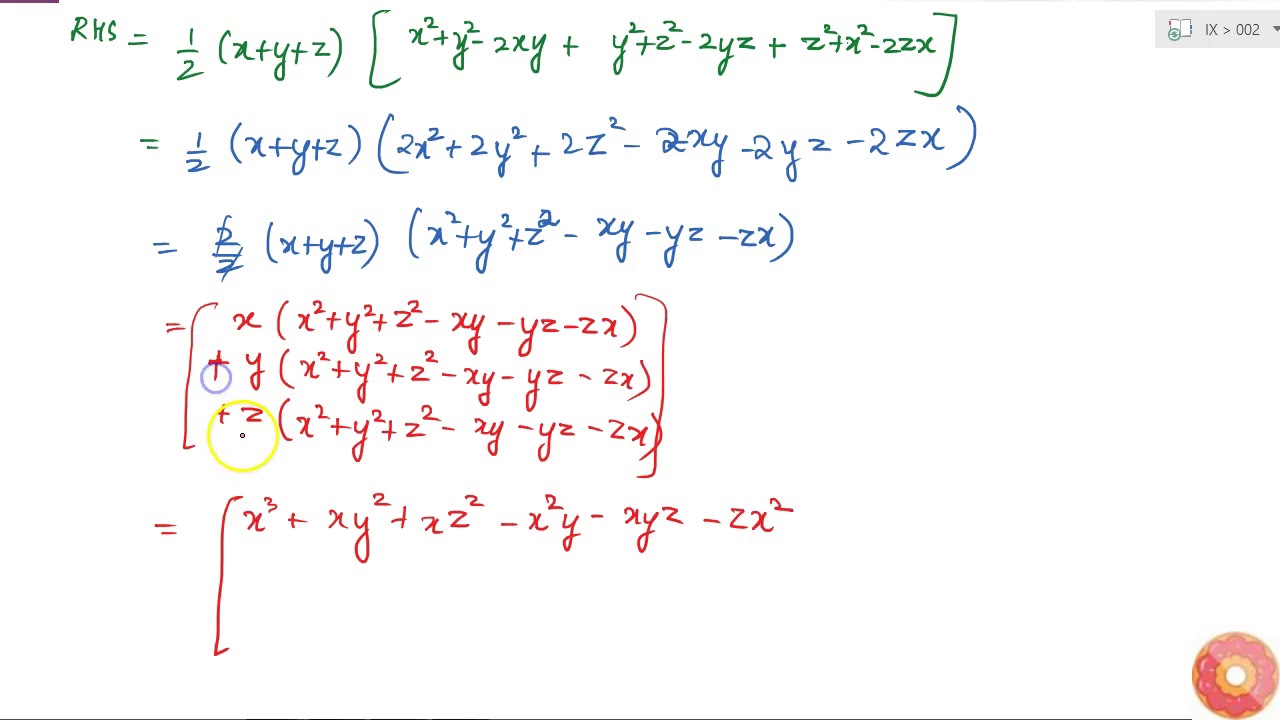



Verify That X 3 Y 3 Z 3 3x Y Z 1 2 X Y Z X Y 2 Y Z 2 Z X 2 Youtube




Ppt Chapter 3 Powerpoint Presentation Free Download Id




Expanding Binomials Video Polynomials Khan Academy
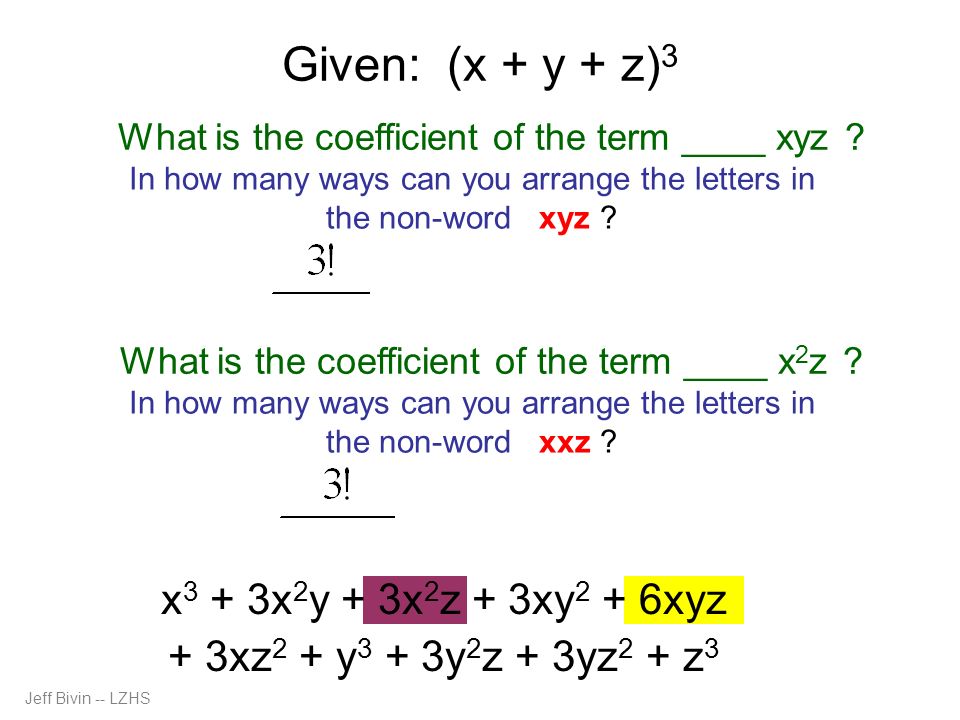



Binomial Expansion And More Ppt Download




Ex Convert The Boolean Function F X Y Z Into A Sum Of Minterms By Using A Truth Table Pdf Free Download



Xyzviewer Xyz File Format Visualiser Calistry



Bench Art Xyz Design




Slides Show



Math In Lwarp Via Controlled Expansion Tex Latex Stack Exchange




Dragon Ball Xyz Chapter 3 Page 40 By Ssgss8goku On Deviantart




Sample Exam 1 Solution Digital Logic Spring 03 Ece 240 Docsity




Math Task 3



The Number Of Terms In The Expansion Of X Y Z N Studyrankersonline




Top 10 Strongest Rank 10 Xyz Monsters In Yu Gi Oh Hobbylark




Xyz Wings And Wxyz Wings Systematic Sudoku




Let X Y Z Be Real Numbers Satisfying X Y Z 3 X 2 Y 2 Z 2 5



1




Xyz Affair Wikipedia




Social News Xyz
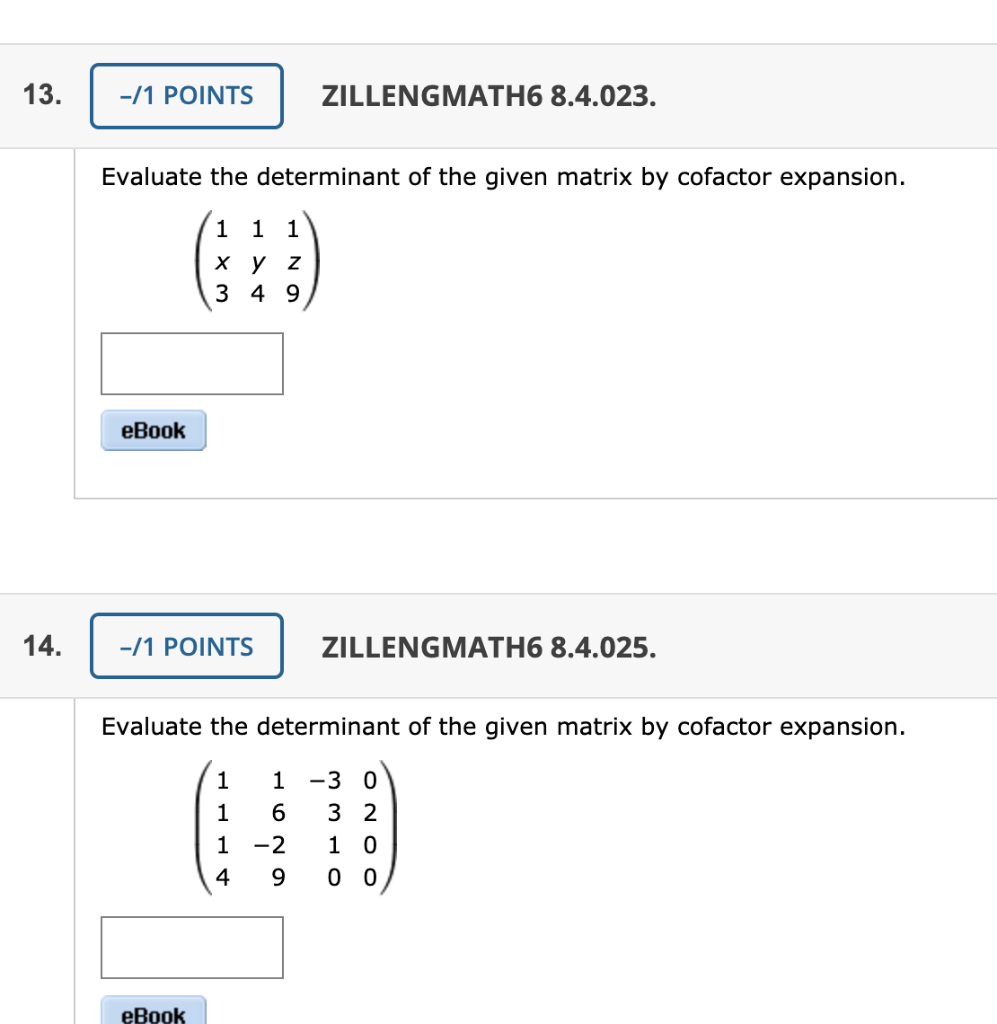



13 1 Points Zillengmath6 8 4 023 Evaluate The Chegg Com



Cubic Expansion Eylemmath



Build A Circuit Using Or Gates And Gates And Inverters That Produces An Output Of 1 If A Decimal Digit Encoded Using A Binary Coded Decimal Expansion Is Divisible By 3 And




Top 10 Rank 7 Xyz Monsters In Yu Gi Oh Hobbylark



Modular Xyz Xpansion Pins Mitee Bite Products Llc




View Question Binomial Theroem




If N Is An Odd Positive Integer And X Y Z Are Distinct Then The Number Of Distinct Terms In Youtube



Depts Washington Edu Simuw Current Pdf Prob Simuw Pdf




Xyz Import Dragons Of Legend The Complete Series Yugioh Tcgplayer Com




Product Share In Customer Wallet Case Study Xyz Bank Information Pdf Powerpoint Templates




Solved Using Shanon S Expansion Find Least Cost Implementation Function F X Y Z M 1 2 3 7 Using 2 Q



1




Wemadeit Xyz Facebook




Pba Expansion Team Nlex Remains Optimistic Despite Being Denied Of A Direct Hire Right Philnews Xyz



Doom 3 Resurrection Of Evil Dlc Eu Steam Cd Key Gaming Xyz




How Can We Put That Whole As 3xyz Why And How Do We Know Maths Determinants Meritnation Com




Part 5 Xy Wings Xyz Wings By Dan Lekander Thousand Islands Life Magazine Thousand Islands Life Magazine All Archives
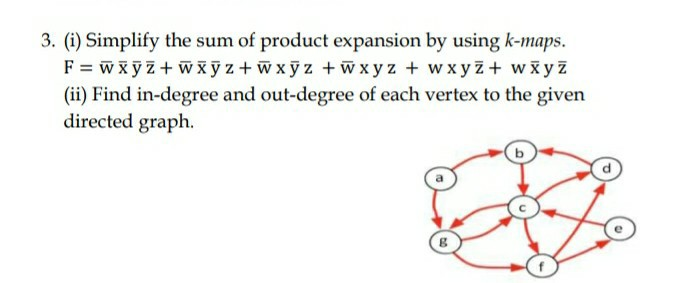



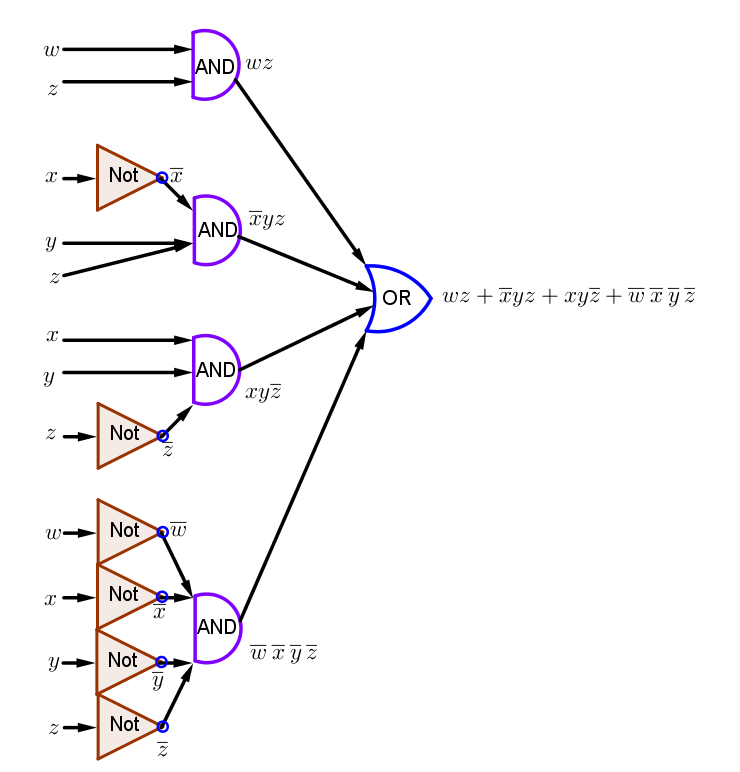
Solved 3 I Simplify The Sum Of Product Expansion By Us Chegg Com



Nfsmods Nfsc Race Expansion Pack 2 101




Slides Show




A Generalization Of Planar Pascal S Triangle To Polynomial Expansion And Connection With Sierpinski Patterns Semantic Scholar




Pocketfm Plans Expansion Of Operations Social News Xyz



What Is The Formula Of Math X 3 Y 3 Z 3 3xyz Math Quora




X Y Z 3 Expand Novocom Top




X Y Z 3 Expand Novocom Top



Digoo Sb Xyz Wireless Bluetooth And Wifi Smart Home Hd Video Doorbell Mullally S Electronics




Table 3 From Advanced Surface Laminar Circuit Packaging With Low Coefficient Of Thermal Expansion And High Wiring Density Semantic Scholar




What Is The Expansion Of A B C 3 Quora




Mitee Bite 0 5 0 025 Xyz Expansion Press Fit Pin




Parallel Tile Calculation In Special Xt Expansion To The Xyz Is Made Download Scientific Diagram
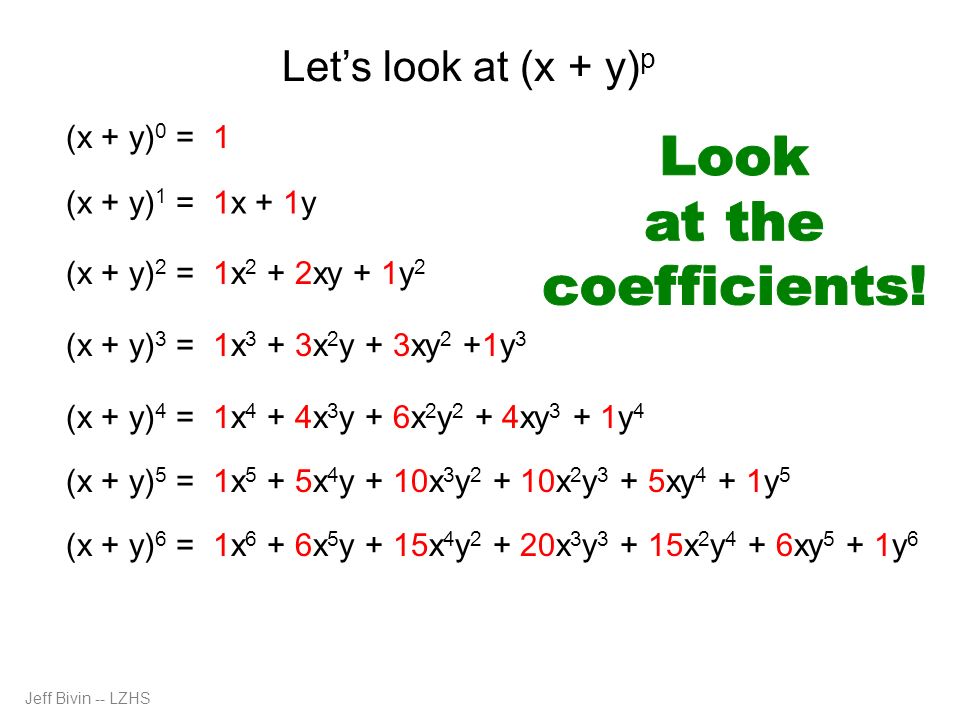



Binomial Expansion And More Ppt Download



2



Solved Find The Sixth Term Of The Binomial Expansion Course Hero




2n U Luese The Coefficient Of X Y Yzt And Xyz T In The Expansion Of X Y Z T Are In The Ratio A 4 2 1 B 2 4 1 11 2 4 D 2 3 4




Modular Xyz Xpansion Pins Mitee Bite Products Llc



Expanding Polynomial Factors Maths First Institute Of Fundamental Sciences Massey University




In The Expansion Of X Y Z A Coefficient Of X 7y 8z 7 Is Zerob Total Number Of Distinct Terms Is 231c Every Term Is Of The Form Frac X R Y R K Z K Left Rright Left R Kright K D Sum Of Coefficient Is 3



What Is The Formula For X Y Z 3 Quora




Arc Rebellion Xyz Dragon Phantom Rage Yugioh Tcgplayer Com




Answered 1 0 1 1 0 07 2 Given A V 1 1 1 1 Bartleby
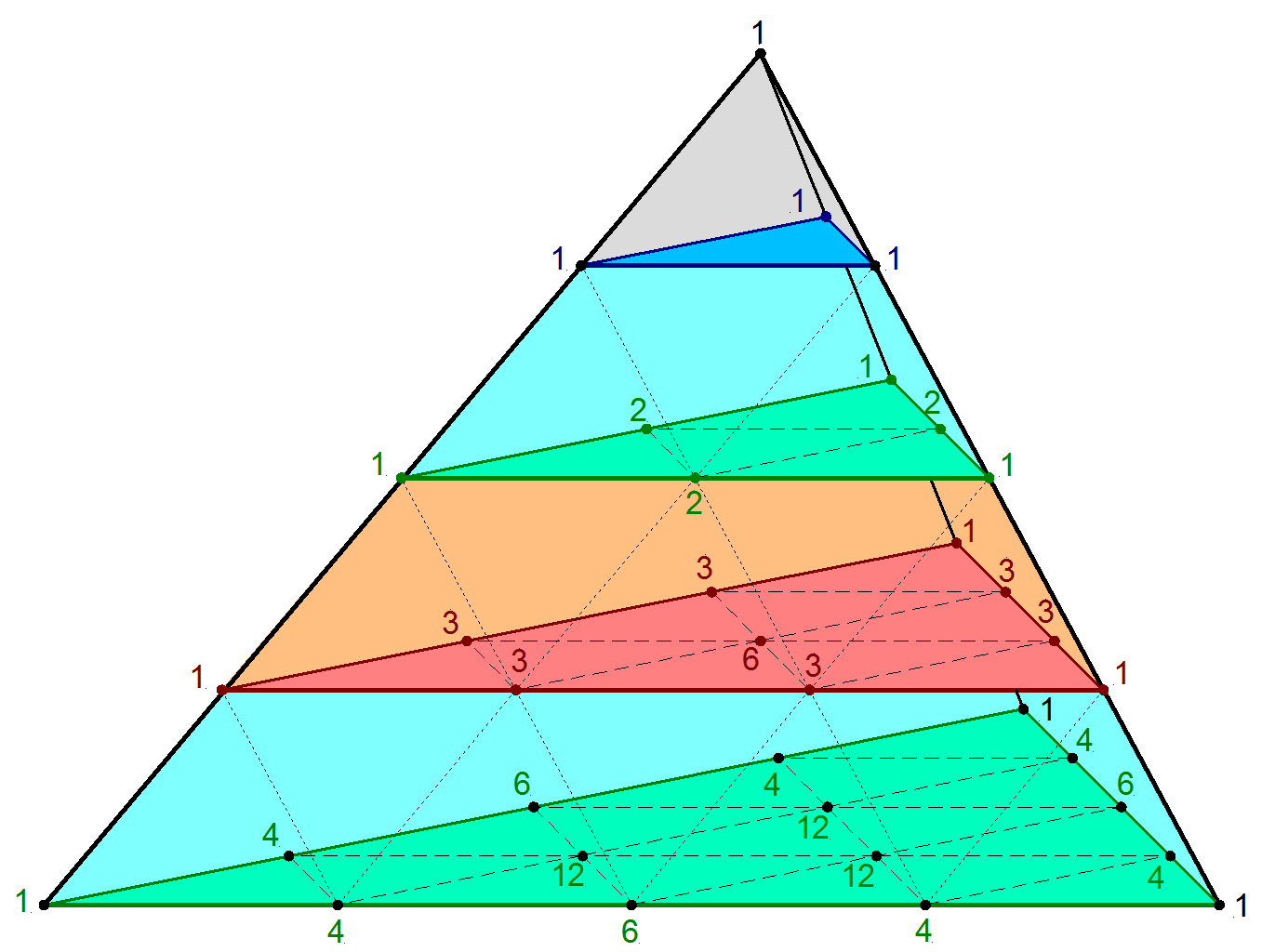



Pascal S Pyramid Wikipedia




Mit Lincoln Laboratory Xyz 3 11 05 Introduction To A Wait Free Hash Table Hash Table Key Value Pair Stores And Retrieves Data Three Core Functions Ppt Download
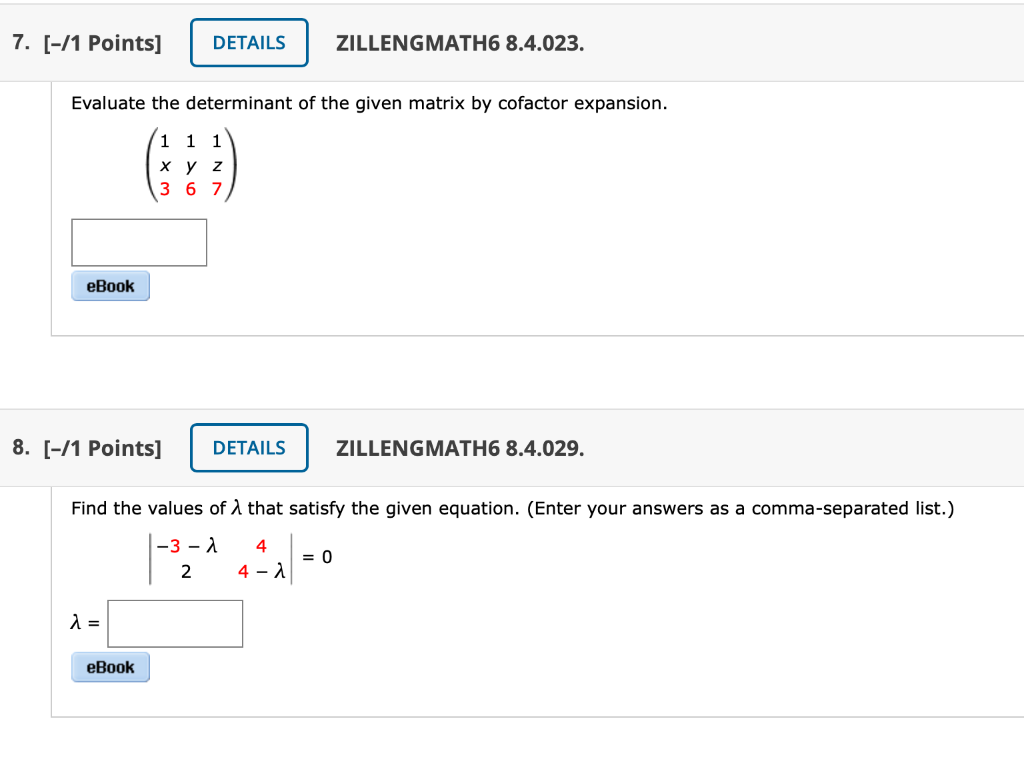



7 1 Points Details Zillengmath6 8 4 023 Chegg Com



Investor Presentation For Society Funding Geographic Expansion Strategy Ppt Powerpoint Presentation Gallery Template Pdf Powerpoint Templates




Expansion Of X Y 3 Y Z 3 Z X 3 Is What Brainly In




Solved Using Shanon S Expansion Find Least Cost Implementation Function F X Y Z M 1 2 3 7 Using 2 Q




Solved 3 5 Use A K Map To Find A Minimal Expansion As Chegg Com




Write The Expanded Form Of X Y Z 3 Brainly In



0 件のコメント:
コメントを投稿