Differential Equation Calculator The calculator will find the solution of the given ODE firstorder, secondorder, nthorder, separable, linear, exact, Bernoulli, homogeneous, or inhomogeneous Initial conditions are also supported Your input solve $$$ y ' \left (x \right) = x^ {2} $$$(c) y00 xy2y0 −y3 = exy is a nonlinear equation; In this section we introduce the method of undetermined coefficients to find particular solutions to nonhomogeneous differential equation We work a wide variety of examples illustrating the many guidelines for making the initial guess of the form of the particular solution that is needed for the method

Deber No 9 Solucion En Serie De Potencias En Torno A Puntos Singulares Ensenanza De Matematica
(1-x^2)y''-2xy'+6y=0
(1-x^2)y''-2xy'+6y=0-Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history1 dy 2y = 0 dx Definimos el factor integrante p (x) = 2 ´ factor integrante e 2dx = e2x multiplicamos la ecuacion por el factor integrante dy e2x dx 2e2x = 0 el lado izquierdo de la ecuacion se reduce a d 2x dx e y =0 separamos variables e integramos ´ d 2x ´ dx e y =0 dx c e2x y = c y = ce−2x 2 dy = 3y dx forma lineal dy




Engineering Mathematics Notes
Sección 61 Reposo de las series de potencias;29 Show that y1 = x2 and y2 = x3 are two different solu tions of x2 y"4xy' 6y = 0, both satisfying the initial conditions y (0) = 0 = y' (0) Explain why these facts do not contradict Theorem 2 (with respect to the guaranteed uniqueness) 30 (a) Show that Yl = x3 and yz = lx3 1 are linearly inde Q727 27 Find a power series in \(x\) for the general solution of \(1x^2)y''4xy'2y=0 \tag{A}\ Use (a) and the formula \{1\over1
En otras palabras, cuando x está en el intervalo de6C3 For the ODE y 2xy 2y = 0, a) find two independent series solutions y1 and y2;Zill Differential Equations 9e Chapter 1 Form B 13 Determine a region of the xy−plane for which the given differential equation has a unique solution passing through a point (x0,y0) in the region (x −1)2(y 2)y′ = 1 14
Question Find The Solution Of Legendre's DE(1x^2)y''2xy'6y=0 Give The Solution Asy=c0all The The Termsc13 Tarms Here This problem has been solved!1 B ` AI T ˆ A P PHU O NG TR ` INH VI PH ˆ AN 1) 2xy y" = y 2 − 1 HD gia ' i y = p 2xpp = p 2 − 1 x(p 2 − 1) = 0 2pdp p 2 − 123doc thư viện trực tuyến, download tài liệu, tải tài liệu, sách, sách số, ebook, audio book, sách nói hàng1 x2 Multiplying through by µ leads to the equation (3 y x2)dx(y − 1 x)dy = 0, which is exact There exists a function F which satisfies ∂F ∂x = 3 y x2, ∂F ∂y = y − 1 x (1) The first of these implies F(x,y) = 3x− y x g(y) Differentiating with respect to y and comparing the result with the second equation in (1) leads to



Http Www Iitg Ac In Jiten Lectures Lec15 Pdf




Math Infinity Differential Calculus Facebook
(b) 4x2y′′ (2x4 − 5x)y′ (3x2 2)y = 0 Solution (a) A0 = lim x→0 A(x) = lim x→0 xP(x) = lim x→0 cos2x−1 x2 = lim x→0 −2sin2x 2x = −2 B0 = lim x→0 B(x) = lim x→0 x2Q(x) = lim x→0 2 = 2 The indicial equation is r2 (A0(1) x2y00 2xy0 −2y =0; Use the method of undetermined coefficients to solve (1x 2 )y′′ – 2xy′ 6y = 0 Using the method of undetermined coefficients obtain a recursion formula relating the terms to the terms Give an explicit formula for for each and find the sum of the series Since this sum is equal to 0, we know that every coefficient of every power




Multiply X 2 4y 2 2xy 3x 6y 9 By X 2y 3
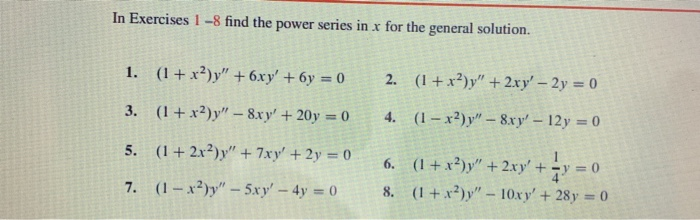



In Exercises 1 8 Find The Power Series In X For The Chegg Com
On the other hand, when the power series is convergent for all x, we say its radius of convergence is infinity,C) express the solution satisfying y(0) = 1, y (0) = −1 in terms of y1 and y2;Exam 1 Review Questions and Answers Part I Finding solutions of a given differential equation 1 Find the real numbers r such that y = ex is a solution of y00 −y0 − 30y = 0 Answer r = 6, −5



Http Www Math Uiuc Edu G Choi1 285finalreviewsol 03 Pdf



Http Www Tccollege Org Wp Content Uploads 19 08 Mathematics Mat4105 O D E M Sc Pdf
1 = x2 is a solution to the differential equation x2y00 2xy0 6y = 0, find a second linearly independent solution using the formula seen earlier Example Given that y 1 = x2 is a solution to the differential equation x2y00 2xy0 6y = 0, find the general solution to the differential equation using the substitution y 2(x) = u(x)y 1(x) 4 Hint Assume that a polynomial of the form y ( x) = x n a n − 1 x n − 1 ⋯ a 0 satisfies the ODE, and pug it in the ODE Then you shall find that n = 2 Next, you shall find that y = x 2 − 1 / 3 Observe that if y is a solution, then so is c y, for every c ∈ R Satisfaction of the condition y ( 1) = 2, implies that the soughtD) express the series in terms of elementary functions (ie, sum the series to an elementary function)




Differential Equations Class 12 Ncert Solutions




Calc Solutions Sec 2 5
Homework Statement Determine the IVP has bounded solution Legendre equation (1x^2)y''2xy'6y=0 ;This particular number ρ is called the r adiu s of c onv er ge nc e Remark 3 The number ρ is at least 0, as taking x = x0 gives P 0 which is clearly converging to 0;X (1 x 2y 2) = 0 , and (**) x = 0 or 1 x 2y 2 = 0 If x=0 in the original equation (x 2 y 2) 2 = 2x 22y 2, then (0y 2) 2 = 02y 2, y 4 2y 2 = 0 , y 2 ( y 2 1 ) = 0 , and y=0 Note, however, if x=0 and y=0 are substituted into Equation 1, we get the indeterminate form " 0/0 " Is y'=0 at the point (0, 0) , ie, does y'(0, 0) = 0




Solutions To Implicit Differentiation Problems




Assignment 1
9 Find general solution of the following di erential equations given a known solution y 1 (i) (T) x(1 0x)y00 2(1 2x)y 2y= 0 y 1 = 1=x (ii) (1 2x)y00 2xy0 2y= 0 y 1 = x Solution (i) Here y 1 = 1=x Substitute y = u(x)=xto get (1 x)u00 2u0= 0Thus, u0= 1=(1 x)2 and u= 1=(1 x) Hence, y1) x 2 y" 3xy' (1 2x)y = 0 about the point x = 0 Solution This equation has a regular singular point at x = 0 Step 1 Assume solution Assume a solution of the form 2)Find second solution to {eq}x^22xy"6y=0 {/eq} given that {eq}y1=x^2 {/eq} Solution of differential equation The given differential equation is a second order linear differential equation



Http Www Uwyo Edu Spitler Courses 2310 317 Pdf Textchap3problems Pdf




Answered Given Legendres Equation 1 A Y Bartleby
To ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `(2xy1)dx(2yx1)dy=0`The equation math\displaystyle{ (1x^2)y'' 2xy' 2y = 0 }\qquad(1)/math Since we have no obvious way to find any particular solution of (1) so we should try to find its general solution in the form of a power series as follows math\displHomework 5 Solutions 3132 f(x;y)=œ xy(x2−y2) x2y2 (x;y)≠(0;0) 0 (x;y)=(0;0) Note fis continuous, (by computing lim(x;y)→(0;0) of the formula above, eg using polar coorinates) (a) Find f x and f y when (x;y)≠(0;0) Away from (0;0);fcan be di erentiated using the formula de ning it,




Identify The Differential Equation Solved By Y Chegg Com



Matematikcimehmetyavuz Files Wordpress Com 15 04 M V Makarets V Yu Reshetnyak Ordinary Diffe Pdf
p ( x 0) ≠ 0 for most of the problems If a point is not an ordinary point we call it a singular point The basic idea to finding a series solution to a differential equation is to assume that we can write the solution as a power series in the form, y(x) = ∞ ∑ n = 0an(x − x0)n y ( x) = ∞ ∑ n = 0 a n ( x − x 0) n (2) Integrate both sides again v = C1 4 x4 C2 Now the general solution is given as y2 = v(x)y1 y2 = ( C1 4 x4 C2)( 1 x) y2 = (C1( x3 4) C2( 1 x)) Now the first solution is given when C1 = 0, then the second solution can be when C2 = 0 which is x3 4 otherwise there are infinite solutionsby just filling the constants To check Exercise 32E 27 (a) Find a power series in x for the general solution of (1 x2)y ″ 4xy ′ 2y = 0 (b) Use (a) and the formula 1 1 − r = 1 r r2 ⋯ rn ⋯ ( − 1 < r < 1) for the sum of a geometric series to find a closed form expression for the general solution of (32E4) on (




Solve The Differential Equation 1 X Y 2xy 6y 0 By Using The Series Solution Method Homeworklib




Calameo Algebra 2 Mcgraw Hill 08
Soluciones en forma de series de potencias 249 W Convergencia absolutaDentro de su intervalo de convergencia, una serie de poten cias converge absolutamente;Ex3 x 2 y''2xy'6y=0 with given solution y 1 =x 2 Take this link after you've tried it yourself ****assignment**** Chapter 4 section 2 Problems 1,3,5,7,171 x2 0 Z 1 z x2 f(x;y;z)dydzdx 10 (15 points) Spherical coordinates Convert the triple integral Z 2 0 Zp 4 x 2 0 Zp 8 x y2 p x 2y xzdzdydx to spherical coordinates (It will help to draw a quick sketch of the threedimensional region of integration) Do not evaluate Solution We have Z ˇ=2 0 Z ˇ=4 0 Z 2 p 2 0 (ˆsin˚cos )(ˆcos˚)(ˆ2



微分方程式が解けません 1 y 5y 6y 0 y 0 0 Yahoo 知恵袋



Http Www Math Colostate Edu Gerhard M345 Chp Ch2 6 Pdf
Y(0)=0, y'(0)=1 Homework Equations P_2122 Behavior of the Solutions 179 Example 126 Find the solution y y x of y 2y 5y 0, with the initial values y 0 2 y 0 1 The auxiliary equation r2 2r 5 0 has the solutions rThis equation cannot be written in the form (1) Remarks on "Linear" Intuitively, a second order differential equation is linear if y00 appears in the equation with exponent 1 only, and if either or both of y and y0 appear in the equation, then they do so with exponent 1 only




1a Engineering Mathematics Ppt Download




Problem 1 Consider The Legendre Differential Chegg Com
Free system of equations calculator solve system of equations stepbystepY 1(x)=e − b 2a x con a, b, c constantes y b2 −4ac =0 canekuammx 21/ 4/ 03 1Steps Using the Quadratic Formula = { x }^ { 2 } { y }^ { 2 } 2xy1=0 = x 2 y 2 − 2 x y − 1 = 0 All equations of the form ax^ {2}bxc=0 can be solved using the quadratic formula \frac {b±\sqrt {b^ {2}4ac}} {2a} The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction



Solved Determine Singular Points Of Each Differential Equation And Classify Each Singular Point As Irrequier Regular A X 4 4xy 3y 0 B Course Hero




Extra Problems With Solutions For Notes On Diffy Qs Section 0 2 Manualzz
(a) x3y′′ (cos2x−1)y′ 2xy = 0;B) determine their radius of convergence;Y 1(x)=e−2x (4) x2y00 xy0 x2 − 1 4 y =0;




Y 2xy E X Dx E Xdy 0 Novocom Top



Series Solution Differential Equations Example 2 Youtube
Technical University of ValenciaY1(x)=x− 1 2 senx (5) ay00 by0 cy =0;I think it's reasonable to do one more separable differential equation from so let's do it derivative of Y with respect to X is equal to Y cosine of X divided by 1 plus 2y squared and they give us an initial condition that Y of 0 is equal to 1 or when X is equal to 0 Y is equal to 1 and I know we did a couple already but another way to think about separable differential equations is really all



6 1 23 Find Power Series Solutions Of X 2 2 Y 3xy Y 0 De Youtube




Thomas Calculus 12th Edition Thomas Solutions Manual
Y 1(x)=x−1 (3) (2x1)y00 4xy0 − 4y =0;Nov 04, 11 Math 334 Fall 11 Homework 8 Solutions Basic Problem 1 Find the general solution for the following a) x2 y′′ 4xy′ 2 y =0 b) x2 y′′ 5 xy′ 4 y =0 c) 2 x2 y′′ 3xy′ 4 y =0 Solution a) Set y= xr we reach r (r − 1)4r 2=012 ECUACIONES DE PRIMER ORDEN 5 Definición 16 Ecuaciones diferenciales exactas La ecuación diferencial M(x,y)dx N(x,y)dy = 0 es exacta si existe




Math 432 Hw 2 5 Solutions Pdf Free Download



Solve The Initial Value Problem In The Case Assume Math X 0 Math Math X 2y 2xy 6y 10x 2 Y 1 1 Y 1 6 Math Homework Help And Answers Slader
Unlock StepbyStep (x^2y^21)^3x^2y^3=0 Extended Keyboard ExamplesView dedocx from MATH 010 at Technological Institute of the Philippines Patricia Anne Manabat CH21F 1 y''6y'13y=0 (pr13, p13, case 3) 2 d2 y dy −4 4 y=0 (pr23, p13, caseTo find solution for the differential equation {eq}x^2y''3xy'=0 {/eq} we can begin by dividing both sides by {eq}x^2 {/eq} and then find the necessary integration factor to multiply the equation by
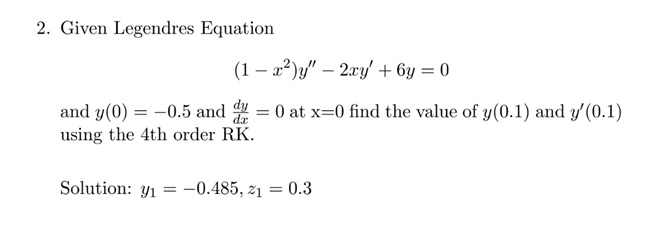



Solved 2 Given Legendres Equation 1 22 Y 2xy 6y Chegg Com




Ad Eng Math 6 8 15 Pages 51 100 Flip Pdf Download Fliphtml5
Steps Using the Quadratic Formula (y1) { x }^ { 2 } 2xyy1=0 ( y − 1) x 2 − 2 x y y 1 = 0 All equations of the form ax^ {2}bxc=0 can be solved using the quadratic formula \frac {b±\sqrt {b^ {2}4ac}} {2a} The quadratic formula gives two solutions,Solution 1 First assume y 2 =ux 2, and y 2 '=2uxu'x 2 and y 2 ''=u''x 2 4u'x2u Substituting into x 2 y''2xy'6y=0 we get x 2 (u''x 2 4u'x2u)2x(2uxu'x 2)6y=0 and simplifying by adding like terms we get u''x 4 6u'x 3 =0 We reduce the order by w=u' to get w'x 4 6wx 3 =0 Now dividing by wx 4 and rearranging, we get and integrating bothY 1(x)=x (2) x2y00 3xy0 y =0;




02e First Order First Degree Reducible To Exact Studocu



Faculty Math Illinois Edu Jpascale Courses 12 M427k Notes Final Practice Sol Pdf




Thomas Calculus 12th Edition Thomas Solutions Manual



R D Sharma Solutions Class 7 Math Chapter 7 Algebraic Expressions Exercise 7 2




Legendre Differential Equation Of Order Two 1 Chegg Com
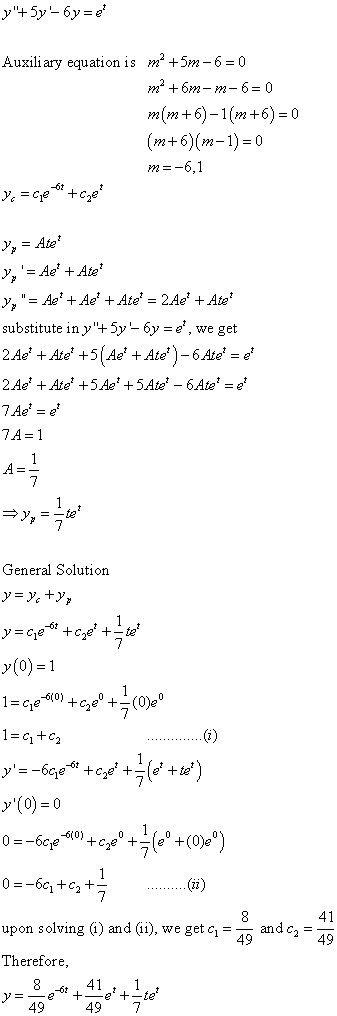



Differential Equations Solved Examples October 17




Engineering Mathematics Notes



Use The Method Of Undetermined Coefficients To Solve 1 X2 Y 2xy 12y 0 Stumbling Robot




Ad Eng Math 6 8 15 Pages 51 100 Flip Pdf Download Fliphtml5



2




El Blog De Jair Beltran Ecuaciones Diferenciales Series De Potencia




Ode 10th Edition Book By Johntss124 Issuu
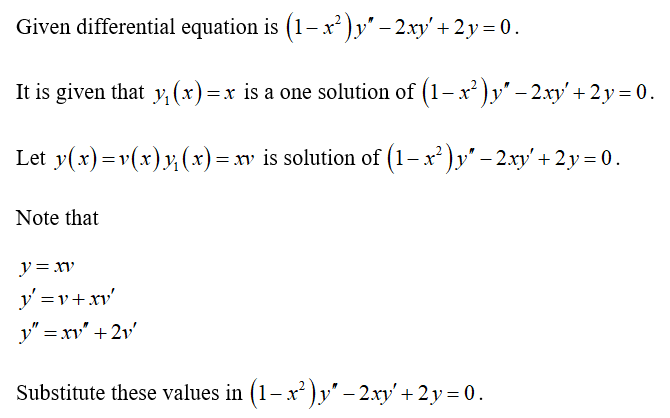



Answered First Note That Yi X X Is One Bartleby




Y 1 X 2 Y 0 Novocom Top




What Is The Solution To The Differential Equation Math 1 X 2 Y 2xy 2y 0 Math Quora




Solved 4 Consider The Differential Equation 1 X2 Y Chegg Com



2




Example 17 Show 2y E X Y Dx Y 2x Ex Y Dy 0 Particular




Use The Reduction Of Order Method To Solve The Following Problem Given One Of The Solution Y1 A X 2 1 Y 39 39 2xy 39 2y 0 Y1 X B 2x 1 Y 39 39 4 X 1 Y 39 4y 0 Y1 E 2x C X




Engineering Mathematics Notes




Respostas Anton Calculo I Cap 04 Calculo Diferencial E Integral Docsity



2



2 X Y 3 X 2 Y 3 Zonealarm Results



Use The Method Of Undetermined Coefficients To Solve 1 X2 Y 2xy 6y 0 Stumbling Robot




Y 2xy E X Dx E Xdy 0 Novocom Top




3x 2y 2xy 1 X 2 Y 7 6 Brainly In



Http Www Math Miami Edu Dscheib Teaching Fall11 Map2302 Files Map2302 Suggested Homework Problems Files Section 3 1 hw Pdf



Q Tbn And9gcqct6yhlglf0yxmagnbx406v2c9rgxehm2s3le V4epdeiz1tex Usqp Cau
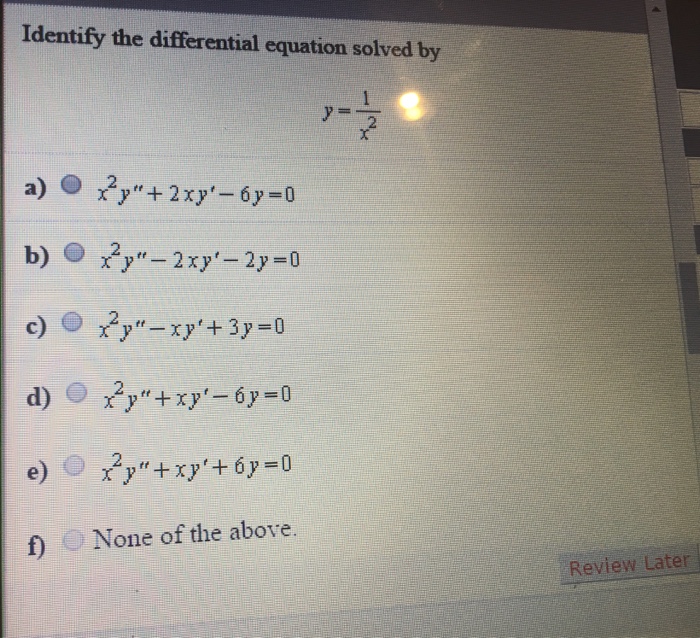



Identify The Differential Equation Solved By Y Chegg Com




Harder Series Solution Differential Equation Y 2xy 8y 0 With In Differential Equations Math Videos Solutions



Matematikcimehmetyavuz Files Wordpress Com 15 04 M V Makarets V Yu Reshetnyak Ordinary Diffe Pdf




Ma 17 3 Complex Analysis Rates



Use The Method Of Undetermined Coefficients To Solve 1 X2 Y 2xy 6y 0 Stumbling Robot



Http 1 160 97 198 8080 Xmlui Bitstream Handle 2 2 chapter 1 11 Pdf Sequence 2




Polynomial Solution Of The Equation 1 X 2 Y 2xy 6y 0 Mathematics Stack Exchange




Pdf Complete Solutions Differential Equations With Modeling Applications Differential Equations With Boundary Value Problems 5th Edition Juan Carlos Becerra Linares Academia Edu



Www Tau Ac Il Levant Ode Solution 6 Pdf




De Ordinary Differential Equation Equations




Differential Equations With Boundary Value Problemsa Zill Cullen



Use The Method Of Undetermined Coefficients To Solve 1 X2 Y 2xy 6y 0 Stumbling Robot



Solucionar A La Siguiente Ecuacion De Cauchy Euler 3 2 X 2 Y 15 2 Xy 6y 0 Solucionar La Brainly Lat



3x 2 2xy 2 Dx 6y 2 X 2 3 Dy 0 Sarthaks Econnect Largest Online Education Community




12 Evaluate Theiudegral Int0 See How To Solve It At Qanda




El Blog De Jair Beltran Ecuaciones Diferenciales Series De Potencia




Deber No 9 Solucion En Serie De Potencias En Torno A Puntos Singulares Ensenanza De Matematica




Pdf 4 2 2 4 T 4 2 2 4 X 1 Introduction To Differential Equations Tanveer Ahmed Academia Edu




Quiz4 P




Differential Equations Linear Separable Y 2xy Y Y 2x Ln Y X 2 C Y E X 2 C C 1 E X 2 Ppt Download




Solve The Differential Equation 1 X Y 2xy 6y 0 By Using The Series Solution Method Homeworklib




1a Engineering Mathematics Ppt Download



Www Researchgate Net Profile Mohamed Mourad Lafifi Post How Can Add A New Method To The Solver Of Simulink Attachment 5a355b1fb53d2f0bba44d1f8 As 3a Download Solving Differential Equations Using Simulink Pdf




How To Solve This Differential Equation Math 1 X 2 Y 6xy 4y 0 R T Math Quora



Is There A Legendre Polynomial In This Differential Equation 1 X 2 Y 2xy 6y 0 Quora




Find A Series Solution About The Point X 0 Of 1 X 2 Y 2xy 2y 0 Youtube



Solved Use The Properties Of Legendre Polynomials To Solve The Following Problems A Find The Solution Of 1 X 2 Y 2xy By F X Valid In Course Hero



2




Solved Assignment 6 For Calculus Ii Math 152 Docsity




Given That Y1 X2 Is A Solution Of X2y 2xy 6y Chegg Com




Second Solution For Reduction Of Order X 2 1 Y 2xy 2y X 2 1 Youtube



Solve 1 X 2 Dy Dx 2xy 4x 2 0 Subject To The Initial Condition Y 0 0 Sarthaks Econnect Largest Online Education Community
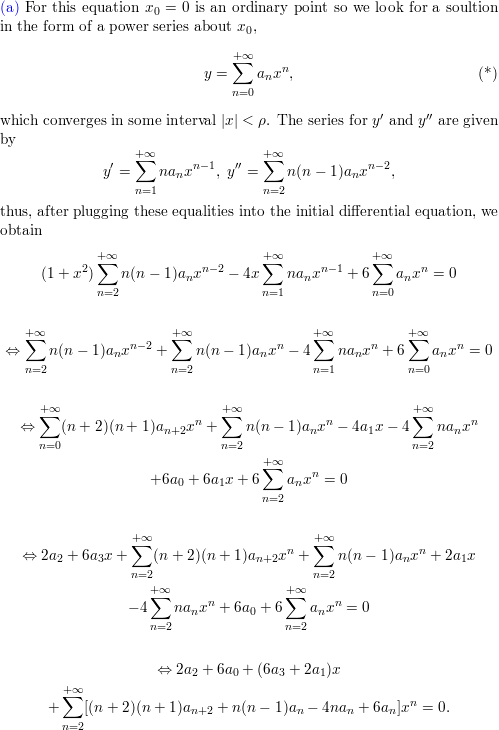



A Seek Power Series Solutions Of The Given Differential Equation About The Given Point X0 Find The Recurrence Relation B Find The First Four Terms In Each Of Two Solutions Y1 And Y2




Math 432 Hw 2 5 Solutions Pdf Free Download
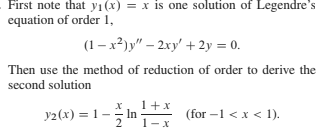



Answered First Note That Yi X X Is One Bartleby




Power Series Solution 1 X 2 Y 4xy 6y 0 Homeworklib




4 A Solve The Differential Equation 1 X 2 Y 2xy L L 1 Y 0 Using Power Series Centered At 0 In Which Homeworklib




Quiz4 P




Math 324 Lecture 2 Math324 1 2 Practice Problems Oneclass




Practice Exercises For Chapter 4 Apple



Http Www Science Marshall Edu Karna Pdfdocfiles Exams 335examssp10 Pdf




Exact Equations Example 3 Video Khan Academy



Matematikcimehmetyavuz Files Wordpress Com 15 04 M V Makarets V Yu Reshetnyak Ordinary Diffe Pdf



0 件のコメント:
コメントを投稿